At equilibrium when ds / dt = 0 and dn / dt = 0:
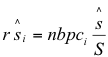
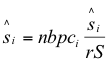
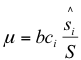
set equations (9) and (10) to zero, and s = s1 c = c1:
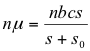
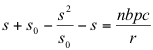
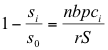
| DERIVATION ASSISTANCE | ||
| equation | notes | text equation |
At equilibrium when ds / dt = 0 and dn / dt = 0: |
||
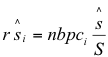 |
(8C) | |
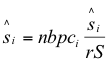 |
(8D) | |
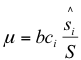 |
(8E) | |
| To derive text equations 11 and 12, the plant growth and herbivore population isoclines, two plant model; set equations (9) and (10) to zero, and s = s1 c = c1: |
||
| |
[from (9)] | (11B) |
| |
(11C) | |
| |
(11D) | |
| |
[equals equation (11)] | (11E) |
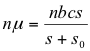 |
[from (10)] | (12A) |
| |
(12B) | |
| (12C) | ||
| |
(12D) | |
| |
[equals equation 12] | (12E) |
| To derive equation 16, the plant growth isocine for logistic plant growth; two plant model: | ||
| (16A) | ||
| (16B) | ||
| (16C) | ||
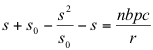 |
(16D) | |
| (16E) | ||
| (16F) | ||
| [equals equation 16] | (16G) | |
| To derive equation 19, equilibrium plant size, multiple plant model. | ||
| [from equations 6 and 8, multiple plant model; D(i) = s / s + s0] | (19A) | |
| [add logistic plant growth] | (19B) | |
| (19C) | ||
| dsi / dt = 0 at equilibrium | (19D) | |
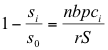 |
(19E) | |
| [equals equation 19] | (19F) | |
| Derive equation 20, herbivore production by plant i, logistic plant growth model. | ||
| [equation 19; cm = ci at si = 0; definition of cm] | (20A) | |
| (20B) | ||
| [definition of P(i); si/S cancels out p] | (20C) | |
| [substitute equation (19)] | (20D) | |
| [substitute equation 20B] | (20E) | |
| [equals equation 20] | (20F) | |
|
||